Simulation of Polymeric Materials : Overview and Examples
1.Introduction
Polymeric materials have multiscale properties ranging from nm to μm in spatial scale, so it is necessary to carefully consider which scale is the origin of phenomena and physical properties. Although many mechanisms have been clarified through the development of experimental and measurement techniques, simulation technology plays an important role in areas that cannot be captured by these approaches alone. In addition, simulation technology also plays a complementary role in the recent progress in the prediction of physical properties using data science.
In the following, we will introduce some of the representative simulation techniques for polymers, their cooperation, software, and so on. The methods are described in order from the smallest scale, as it is easier to understand if we focus on the spatial scale targeted by each method. Since the list of references for each method is endless, we basically refer the reader to the reference [1].
2.Quantum Chemistry & Density Functional Theory
The method mainly targets a few nm or less and calculates electronic states in molecules and crystals based on the Schrödinger equation. It is especially used to evaluate electronic properties of materials such as excitation, polarization, intermolecular forces, and chemical reactions. There is the Molecular Orbital method (MO) and Density Functional Theory (DFT), which can reduce the computational burden by using the electron density as the target of calculation. Each of these methods is subdivided according to how electron correlations are incorporated, how basis functions are chosen, etc. [2].
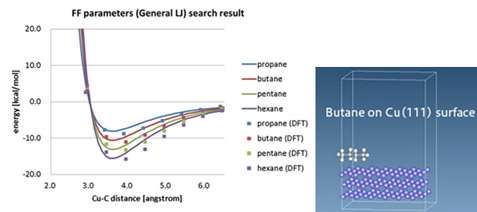 Figure 1. Evaluation of adsorption energy of molecules on Cu surface by DFT
Figure 1. Evaluation of adsorption energy of molecules on Cu surface by DFT
(Left: adsorption energy curves of propane/butane/pentane/hexane molecules; Right: calculated model)
Figure 1 shows the results of DFT calculations (indicated by dots for each molecular species) for the relationship between distance from the surface and energy when molecules are adsorbed on the Cu crystal surface, taking into account the van der Waals force, and fitting to the Lennard-Jones (LJ) potential for use in molecular dynamics The curve is also shown. The surface adsorption energies are important in the design of interfaces, but in some cases there are no reasonable LJ potential parameters, and evaluation by DFT or other methods is necessary.
3.Full Atomistic Molecular Dynamics
In Full Atomistic Molecular Dynamics (FAMD), one particle represents one atom (Figure 2 left), and the dynamics of each particle is calculated based on Newton's equation of motion. The force acting on each atom is given by a function and parameters, including the LJ potential mentioned above. FAMD can be used to evaluate the effect of changes in molecular structure, such as functional groups, on the conformation and dynamics of molecules. Examples are the density and elastic modulus of polymers in the bulk state, the free volume distribution and diffusion of gas molecules within it, and the oriented (crystalline) Structure. FAMD has become popular because of its applicability to a wide variety of applications. On the other hand, as long as general computers are used, the spatial scale that can be handled is about 10 nm, and the time scale is on the order of 100 ns even when using recent software and hardware (such as GPUs). This is insufficient to handle, for example, long-time relaxation phenomena of polymers.
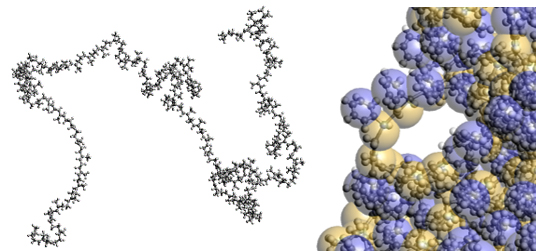 Figure 2. Left: Molecular structure of Polyisoprene by FAMD, Right: CGMD image
Figure 2. Left: Molecular structure of Polyisoprene by FAMD, Right: CGMD image
4.Coarse Grained Molecular Dynamics
In Coarse Grained Molecular Dynamics (CGMD), a single particle represents a group of several atoms (Figure 2, right). For example, when evaluating the tensile properties of rubber materials, it is necessary to perform calculations on a time scale (deformation rate) that can handle the rubber state. This is difficult to achieve with FAMD, but is possible with CGMD. The interaction between coarse-grained units (coarse-grained potential) may be determined based on FAMD [3]. Alternatively, calculations may be performed using simplified parameters and then cross-checked with experimental data (given units such as MPa).
In Figure 3, the behavior of phase-separated structures (thermoplastic elastomers) formed by triblock copolymers such as Styrene-Isoprene-Styrene (SIS) during uniaxial elongation is evaluated [4]. The results of mean-field method calculations, described below, were used to construct the initial structure. The deformation of domains and molecular chains during elongation is captured.
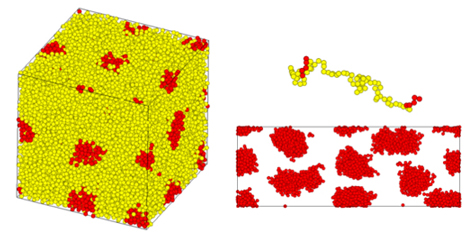 Figure 3. Uniaxial elongation calculations of phase-separated structures of triblock copolymers by CGMD. (left: initial structure, right: structure under deformation (top: single chain, bottom: domain structure))
Figure 3. Uniaxial elongation calculations of phase-separated structures of triblock copolymers by CGMD. (left: initial structure, right: structure under deformation (top: single chain, bottom: domain structure))
5.Dissipative Particle Dynamics and Mean Field method
Dissipative Particle Dynamics (DPD) [5] is one of the CGMDs, but its use of soft potentials that allow particle-particle interactions to slip through makes it suitable for phase separation and the evaluation of filler dispersion structures. Dynamics also includes hydrodynamic effects. In the Mean Field (MF) method, each component of a polymer is represented as a concentration (volume fraction) field to evaluate the dynamics of phase separation and even the equilibrium state. It can be coupled with diffusion and hydrodynamics of each component. In particular, Self-Consistent Field Theory (SCFT) can be used to take into account the shape of polymer chains. In these methods, the Flory-Huggins χ parameter is used as the interaction between components (particles). Methods for estimating this parameter using FAMD and quantum chemical calculations have been proposed [6].
Figure 4 (left) shows the phase-separation structure of polyelectrolyte and water calculated using DPD, and Figure 4 (right) shows the phase-separation (core/shell) structure of a three-component polymer system calculated using the mean-field method. Spatial scales of up to several hundred nm are targeted.
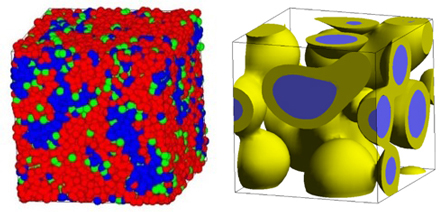 Figure 4. Left: Phase separation structure of polyelectrolyte by DPD,
Right: Phase separation structure of three polymer components by mean-field method
Figure 4. Left: Phase separation structure of polyelectrolyte by DPD,
Right: Phase separation structure of three polymer components by mean-field method
6.Reptation Dynamics
By coarse-graining polymer chains in units of molecular weight between entanglement points, reptation dynamics based on the entanglement structure of polymer chains can be calculated. Methods include the Slip Link model and the Primitive Chain Network (PCN) model. Recently, the Slip Spring model [7] is capable of adding polymer chain entanglement effects to DPD.
Figure 5 is an evaluation of the G' (storage modulus) and G" (loss modulus) of Polyisoprene (molecular weight about 48,800). Bending points in the snapshot corresponds to the entanglement points.
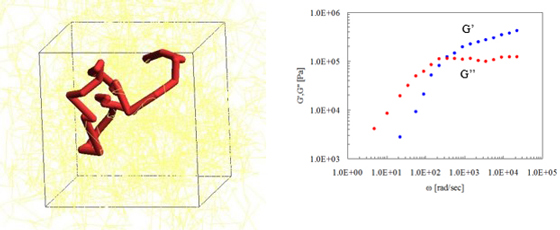 Figure 5. Evaluation of viscoelasticity by PCN (left: snapshot, right: master curve)
Figure 5. Evaluation of viscoelasticity by PCN (left: snapshot, right: master curve)
7.Continuum Model
Using the phase molecular structures obtained by the DPD and mean-field methods, Finite Element Method (FEM) calculations based on continuum models can be performed to evaluate physical properties such as average elastic modulus and thermal conductivity. The material properties of each component are input as parameters. Figure 6 (left) shows the strain energy distribution at the interface when deformation is applied to the phase-separated structure obtained in Figure 4 (right), and Figure 6 (right) shows the heat flux distribution when heat conduction calculations are performed on the nanofiller dispersion structure in the polymer obtained by DPD. The calculation in Fig. 6 is based on a structure obtained by some kind of simulation, but there are other ways to utilize the structure, such as using data from scattering tests or CT instead, or conducting numerical experiments on the relationship between physical properties and structure by creating a virtual structure.
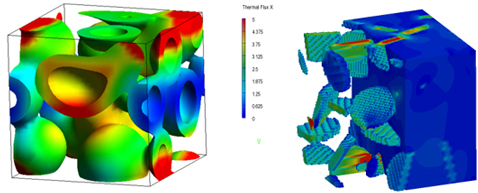 Figure 6. Evaluation of mechanical properties by finite element method
Figure 6. Evaluation of mechanical properties by finite element method
(Left: Strain energy distribution in phase-separated structure, Right: Heat flux distribution in nanofiller dispersed structure)
8.Engines (solvers) included in J-OCTA
For quantum chemistry and density functional theory, SIESTA and ABINIT-MP are bundled, and interfaces to Gaussian and others are provided. For full atomistic and coarse-grained molecular dynamics, COGNAC, VSOP, and GENESIS are included, and interfaces to LAMMPS, GROMACS, and HOOMD-blue are provided. Dissipative particle dynamics (DPD) is similar to molecular dynamics but is not included in GENESIS and GROMACS. SUSHI is included for mean field methods. For reptation dynamics, COGNAC and VSOP's DPD functions with the Slip-Spring model, PASTA, and NAPLES are included. For continuum models, MUFFIN is applicable, and interfaces to other commercial CAE software are also provided.
- Reference
- [1] “Computer Simulation of Polymeric Materials -Applications of the OCTA System-”, Springer (2016)
- [2] R.M.Martin, “Electronic Structure: Basic Theory and Practical Methods”, Cambridge University Press (2004)
- [3] C.Peter and K.Kremer, Soft Matter, 5, 4357 (2009)
- [4] T.Aoyagi and T.Honda, J.Chem.Phys., 117, 8153 (2002)
- [5] R.D.Groot and P.B.Warren, J.Chem.Phys., 107, 4423 (1997)
- [6] K.Okuwaki, Y.Mochizuki, H.Doi, and T.Ozawa, J.Phys.Chem.B, 122, 338 (2018)
- [7] Y.Masubuchi, M.Langeloth, M.C.Böhm, T.Inoue, and F.Müller-Plathe, Macromolecules, 49, 9186 (2016)


