- Full Atomistic MD
- Optical / Electrical / Magnetic
- Materials Science
Dielectric dispersion of water in the GHz frequency range
Purpose and method
We evaluated the dielectric dispersion of water using the full-atomistic molecular dynamics method.
In the case of a material with Debye-type relaxation, a material with one relaxation time, the complex permittivity (ε′ and ε′′) is expressed by the following equation, with τ as the relaxation time.
\[ ε'(\omega) = ε(\infty) + \frac{ε(0) - ε(\infty)}{1 + (\omega\tau)^2} \]
\[ ε''(\omega) = \frac{(ε(0) - ε(\infty))\omega\tau}{1 + (\omega\tau)^2} \]
…（1）
ε\('\) : Real part of complex permittivity
ε\(''\) : Imaginary part of complex permittivity
ε(0) : Static permittivity
ε(∞) : Permittivity caused from displacement polarization
τ is evaluated from the dielectric relaxation function φ(t). φ(t) can be obtained from the time autocorrelation function (Eq. 2) of the dipole moment per unit volume, the polarization P (t).
\[ \varphi(t) = \frac{\langle P(t) ・ P(0)\rangle}{\langle P(0) ・ P(0)\rangle} \]
…（2）
The polarization at each time was obtained by performing equilibrium calculation using VSOP, and the dielectric relaxation function was evaluated by calculating the polarization autocorrelation function. The NVT equilibrium calculation was performed at a temperature of 300 [K] using SPC/Fw for the force field of water.
The relaxation time τ was obtained by fitting the result with the Debye - type relaxation function (Eq. 3).
\[ \varphi(t) = \varphi_0 e^{ - \frac{t}{\tau}} \]
…（3）
Furthermore, based on the equilibrium calculation result of VSOP, ε(0) was obtained from the following formula (Eq. 4).
\[ ε_0 = 1 + \frac{4\pi V}{3k_BT}(\langle P^{2} \rangle - \langle P \rangle^{2} ) \]
…（4）
\( k_B \) : Boltzmann constant
𝑇 : Temperature [K]
𝑉 : Volume
Simulation result
Figure 1 shows the dielectric relaxation function by VSOP. τ was estimated to be 11.3 [ps] by fitting this dielectric relaxation function with the Debye-type relaxation function (Eq. 3).
In addition, 𝜀(0) obtained from Equation 4 is 79.9, which is close to the reference [1] 77.8.
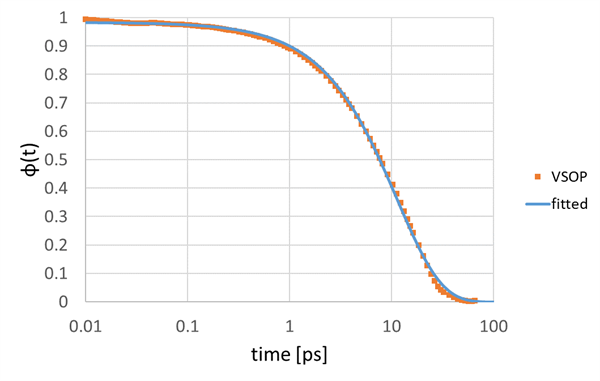Figure 1 The dielectric relaxation of water
Dielectric dispersion was evaluated using these result τ and ε(0) with Equation 1, and shown as Figure 2. In this calculation, we applied 5.85 into ε(∞) based on the reference [2].
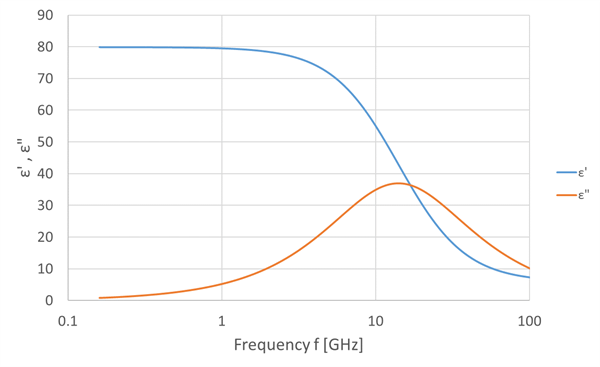Figure 2 The dielectric dispersion of water
- Reference
- [1] Chronological Scientific Tables 2005, published by Maruzen
[2] Liebe, H.J. et al, Int J Infrared Milli Waves 12, 659–675 (1991)
