- Full Atomistic MD
- Thermal
- Materials Science
[Analysis Example] Evaluation of the specific heat with quantum corrections
Specific heat at constant volume is evaluated with higher accuracy.
Objectives and Methods
According to classical thermodynamics, the specific heat at constant volume can be obtained by differentiating the total energy by temperature. When this is applied directly to trajectories obtained by classical molecular dynamics, the specific heat evaluated tends to be overestimated compared to experimental values [1]. In this case, based on the knowledge of quantum statistical mechanics, a quantum correction was applied to the trajectory obtained by classical molecular dynamics[2] to evaluate the specific heat at constant volume more accurately.
The specific heat at constant volume \(C_V\) of a solid can be evaluated using the density of states \(D(\nu)\) and the Bose-Einstein distribution function \(f_{BE} (\nu)\) with the following equation
\[C_V=\frac{\partial}{\partial T}\int_0^\infty E(\nu)D(\nu)f_{BE}(\nu)d\nu\]
where \(T\) is temperature,\(E(\nu)=h\nu\) where \(h\) is the Planck constant and \(\nu\) is the frequency. In classical molecular dynamics, the density of states is obtained by Fourier transforming the velocity autocorrelation function of atoms. A quantum correction is applied to this density of states by multiplying it by the Bose-Einstein distribution function.
Results
This method was applied to 50-mers of polystyrene (PS) and PMMA. L-OPLS was used as the force field, and the velocity autocorrelation function was obtained from the equilibrium NVT calculation at 300 K. The density of states was obtained by Fourier transforming the velocity autocorrelation function.
The density of states of PMMA evaluated from the trajectories obtained by MD is shown in Figure 1. The specific heat at constant volume is evaluated by integrating this density of states with the frequency.
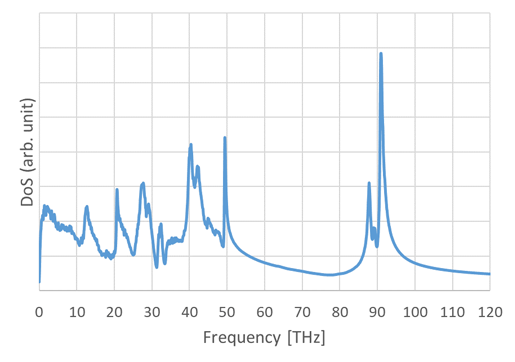Figure 1 Density of state of PMMA evaluated by MD
The specific heat at constant volume for PS and PMMA at 300 K, as evaluated by MD, is shown in Table 1 below. For comparison and reference, the values of the specific heat of constant pressure given in the literature [3] are also shown together.
Table 1: Calculated results of specific heat at constant volume
| Specific heat(J/g/K) | PS | PMMA |
|---|---|---|
| MD（at constant volume, 300K） | 1.29 | 1.45 |
| Reference（at constant pressure） | 1.185 (273.15K) 1.256 (323.15K) |
1.42 (298.15K) |
- Reference
- [1] R. Bhowmika, S. Sihn, V. Varshney, A. K. Roy and J. P. Vernona, Polymer, 167, 176 (2019)
- [2] C. Li, G. A. Medvedev, E. Lee, J. Kim, J. M. Caruthers and A. Strachan, Polymer, 53, 4222 (2012)
- [3] Polymer Handbook 4th Edition, Wiley, New York (1999)
