- Quantum Chemistry / DFT
- Mechanical / Viscosity / Viscoelasticity
- Materials Science
Evaluation of mechanical properties
Purpose and method
Mechanical properties are some of the most fundamental material properties, and evaluation of them are considered to be the first step in investigating material deformation and failure processes. For example, Young's modulus can be calculated from strain ε and stress σ in a uniaxial deformation using Equation (1).
For isotropic materials, the relationship between Young's modulus E, bulk modulus B, and Poisson's ratio ν is expressed as Equation (2).
\[ E = \frac{ σ }{ ε } \]
…（1）
\[ \nu = \frac{ 3B-E }{ 6B } \]
…（2）
In this case study, the Young's modulus, bulk modulus, and Poisson's ratio of Si crystal were calculated using SIESTA. The PBE functional and DZP basis functions are used in the calculations.
Figure 1. The calculation model of Si crystal
Simulation result
The bulk modulus was calculated for the Si model using the EOS workflow of the SIESTA modeler. The relationship between volumes and energies were fitted using an equation of state model for solids, which gave a value of B=89 GPa.
Next, a deformed model in the c-axis of the crystal was created, and the a- and the b-axes were optimized to evaluate stress of the deformed crystal. The amount of strain and the calculated stress values yielded a Young's modulus of 130 GPa. These two values yielded a Poisson's ratio of ν = 0.256. These values are reasonable in comparison with those reported in the previous studies* (E=122-131, ν=0.26-0.28).
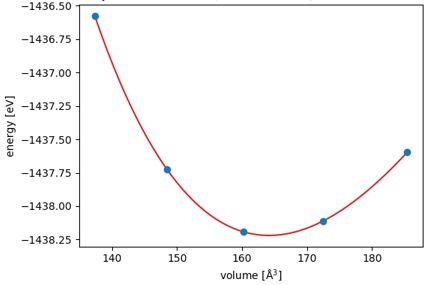Figure 2. Relationship between volume and energy of Si crystals
- Refecence
- B. Lee and R.E. Rudd, Phys. Rev. B, 75, 195328
