- Quantum Chemistry / DFT
- Thermal
- Materials Science
Electronic specific heat analysis of metals
Density of states of metals and specific heat capacity per mole of electrons and electron specific heat coefficient calculation examples
Purpose and method
The electronic specific heat of metal is an important physical quantity to understand the electronic state at very low temperature. From the obtained specific heat, we can estimate the density of states of the Fermi surface and the thermal effective mass of the electrons. The electron specific heat CVel is given by the following equation:
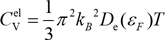
εF: Fermi energy
De(εF) : Density of states at the Fermi surface
From this equation, we can see that the electron specific heat is proportional to the density of states at the Fermi surface. This is because only electrons in the temperature range of a few Kelvin including the Fermi surface, which corresponds to the temperature at the time of measurement at low temperatures, contribute to the electron specific heat. However, the evaluation using the density of states at the Fermi surface, which is calculated numerically in practice, is a rough approximation.
Therefore, in order to take into account the energy dependence of the density of states, we performed the analysis by taking the numerical integration back to the following equation where ƒF(ε) is the Fermi-Dirac distribution function.
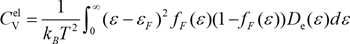
SIESTA modeler allows you to calculate and visualize the density of states. In this section, we will show an example of calculating the density of states for Li, K, Al and Cu metals and determining the specific heat capacity per mole of electrons and the electron specific heat coefficient.
Simulation result
Figure 1 shows the results of the electronic density of states obtained from SIESTA modeler. The red line in the figure indicates the Fermi energy. The electronic specific heat obtained from this density of states is shown in Figure 2. It can be seen that the all specific heat curves change almost linearly. Figure 3 shows a graph of the electronic specific heat coefficient result, which is the electron specific heat at each temperature divided by its temperature, compared to the literature* value.
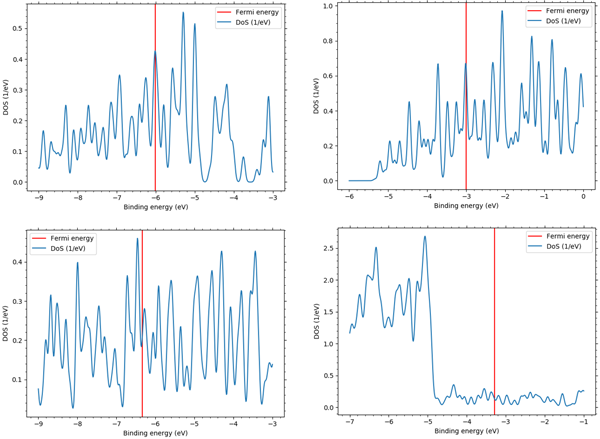Figure1 Electronic density of states for Li, K, Cu and Al, clockwise from top left
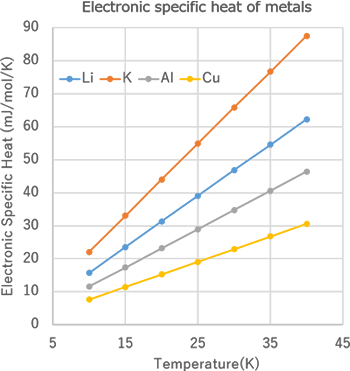Figure2 Temperature dependence of the electronic
specific heat of Li, K, Al and Cu
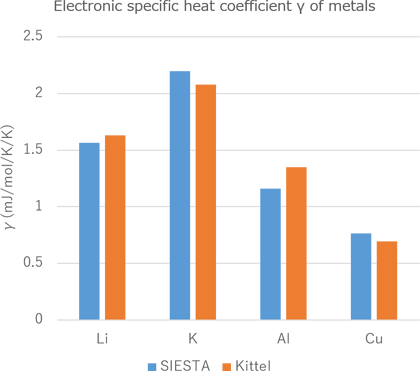Figure3 Electronic specific heat constant of Li, K, Al and Cu
- Reference
- *C. Kittel, Introduction to Solid State Physics, Wiley, 2004
