[Analysis Example] Analysis of ground state and elastic modulus of lithium cobalt oxide

Lithium cobalt oxide is widely used as a positive electrode material for lithium-ion batteries with an intercalate structure, as shown in Figure 1.

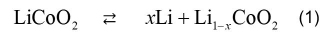
In equation (1), the reaction progresses from left to right during charging, and from right to left during discharging. The possible values of x in the above are 0<x<0.5 (structural transition when x=0.5), and it is known that the electronic state and elastic properties change greatly depending on the value of x. In this case study, we will introduce the analysis results of the ground state and elastic constant of lithium cobalt oxide LiCoO₂ in the discharge state x=0.From the results of the partial density of states shown in Figure 2, as seen in many oxide transition metals, there is a major contribution from the 2p orbital of oxygen and the 3d orbital of cobalt near the Fermi energy, forming an energy gap. This energy gap is estimated to be about 2.1 ∼ 2.7eV ([1,2,3,4]) from previous experiments. In order to represent the localization of electrons in cobalt's 3d orbitals, it is essential to apply the LDA+U method that can appropriately express the localization of electrons due to electronic correlation. In this analysis, the LDA+U method was used to set Hubbard's U (=2.3eV) so that the energy gap was approximately 2.4eV.

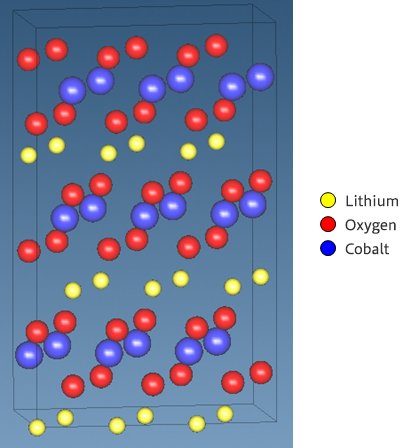Figure 1. LiCoO₂ intercalate crystal

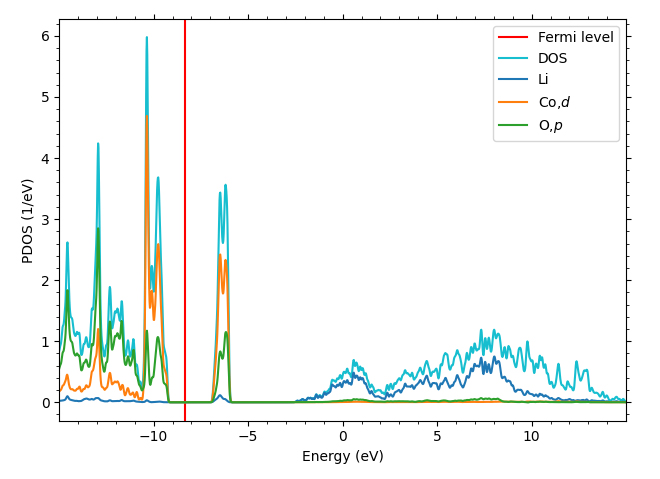Figure２ Partial density of states of LiCoO₂The Fermi energy neighborhood consists of contributions from cobalt's d orbital and oxygen's p orbital.

Figure 3. Initial magnetization state of cobalt
The yellow arrow is an image of the magnetization direction

It is said that the ground state of Li_1-xCoO₂ is a non-magnetic state when x=0, but in this case, for verification purposes, we set the non-magnetic state for cobalt and compared the results with an antiferromagnetic state in the initial state.

We performed two types of shape optimization analysis (relaxation analysis) specifying (Figure 3) and compared the density of states across the Fermi energy.

Figure 4 shows the analysis results comparing the two. It can be seen that both values match within the numerical error range. This shows that in an analysis that even specifies an antiferromagnetic state as the initial state, it converges to a non-magnetic state during the convergence calculation process. This shows that the ground state at x=0 is nonmagnetic.

Figure 5 shows the results of the bulk modulus analysis in this state. In this analysis, the bulk modulus is calculated as the second derivative of the energy change when the cell length on each side is compressed or expanded by up to 1% around the optimized shape obtained above. The analysis results showed that the bulk modulus was 184.73GPa (Voigt), which almost matched the 177.16GPa (Voigt) result from VASP in Table II in Reference [5].

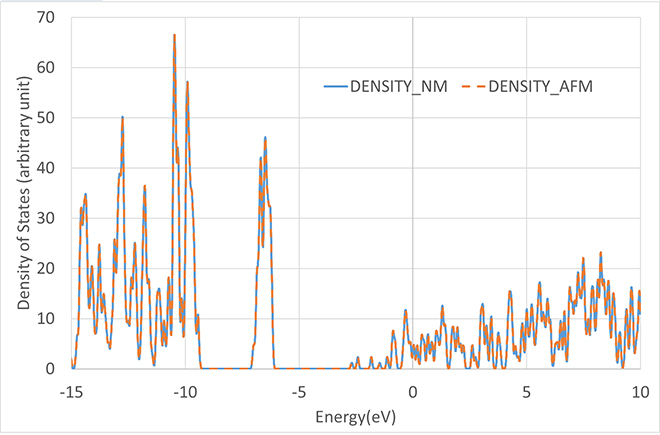Figure 4. Comparison of density of states
DENSITY_NM (Fermi energy -7.9919eV) Result of setting non-magnetic state to cobalt.
DENSITY_AFM (Fermi energy -7.9921eV) Result when competing with antiferromagnetic state as initial state in cobalt.
The difference in Fermi energy cannot be seen on the graph, so it is shown only as a red line.

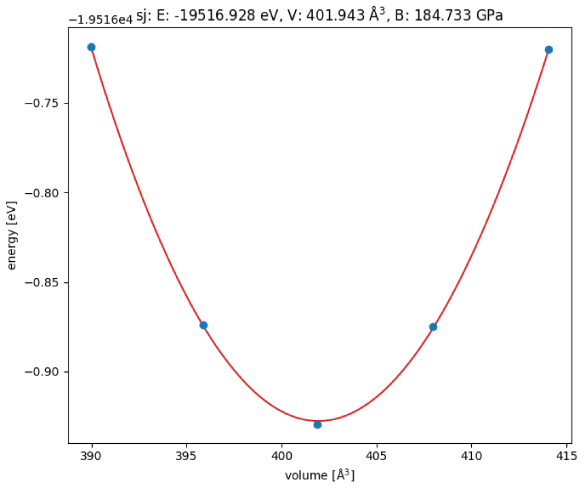Figure 5. Change in energy and bulk modulus during compression or expansion
Bulk modulus is 184.73GPa (evaluation method is equivalent to Voigt).