Overview of First-Principles (ab initio) calculation
Overview and History
First-Principles(ab initio) calculation is a method based on quantum mechanics and quantum chemistry, which are theories about the electronic states of matter. DFT is one of the ab initio methods. Historically, Schrödinger's equations governing the behavior of electrons in 1926 are considered to be the beginning of this field. Later, the Hohenberg-Kohn theorem and the method of Kohn and Sham were proposed about DFT, and the foundations of the theory were established. After 1990, a number of practical functionals were developed, and it was recognized that DFT calculation was actually useful. As a result, in 1998, Kohn and Pople were awarded the Nobel Prize for their significant contributions to the field of computational chemistry, including DFT. Pople is credited with developing Gaussian, a software program for quantum chemistry. Gaussian is also interfaced with many general-purpose molecular simulation software such as J-OCTA.
Position in molecular simulation
Next, the position of First-Principles calculation in molecular simulation will be explained. General-purpose software such as J-OCTA allows the use of various theories and engines (solvers) based on them, from the nanometer scale to the micrometer scale, depending on the scale of the phenomenon (multi-scale simulation).
First-Principles calculation are based on theories that consider the electronic properties of materials and molecules, so they target phenomena at the nanoscale. At this scale, we will treat matter at the atomic level and perform modeling.
In fact, there is also a nano-scale simulation method called all-atom molecular dynamics (Molecular Dynamics : MD), which is sometimes called classical MD in a more limited sense. In J-OCTA, COGNAC, VSOP, LAMMPS, GROMACS, HOOMD-blue, and GENESIS are available. So what is the difference between First-Principles calculation and classical MD calculation?
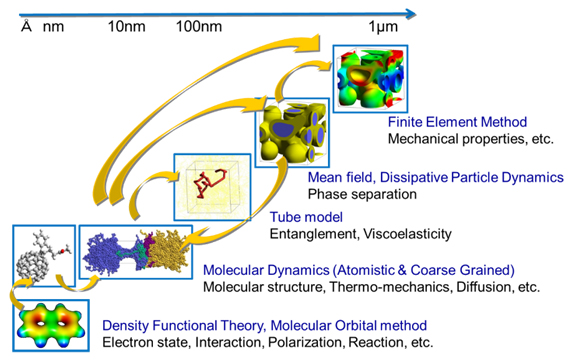Fig.1. Multi-scale (molecular) simulation
Differences from Classical Molecular Dynamics (MD)
In general, molecular dynamics (MD) refers to classical MD, which requires a force field parameter for calculation. Molecular dynamics is the study of the behavior of matter and molecules by calculating the forces acting between atoms using force field parameters. However, the general-purpose force fields that are usually used deal with the ground state and cannot deal with different electron states. When a substance is exposed to light, for example, electrons in the substance can be excited, or the electric field can cause polarization of the electrons. Also, a reaction can occur when a molecule is in close vicinity of another molecule. These excited states, polarization of electrons, and intermediate states in which molecules react are difficult to handle in force field calculations, so first-principles calculation is necessary to consider these situations.
As shown in the figure below, first-principles calculations treat the distribution of electrons explicitly. Therefore, it is quite natural that electron polarization distorts this distribution. In molecular dynamics, electrostatic interaction by electrons is simulated as a point charge. Although the charge is determined in such a way as to give results equivalent to first-principles calculations of electrostatic interactions, it is clear that the distribution of electrons is very different between the two.
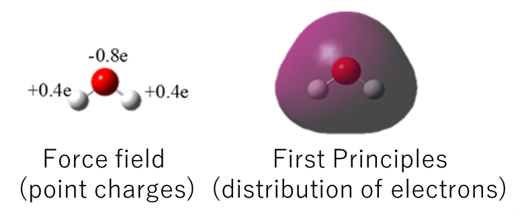Fig.2. Difference between force field calculation and first-principles calculation
Classification of First-Principles calculation
We first mentioned that DFT is one of the First-Principles calculation methods. In the field of First-Principles calculations, there are various calculation methods depending on the method and degree of approximation.
The Hartree-Fock (HF) method has the disadvantage that it cannot incorporate correlations between electrons with the same spin, and the post-HF method attempts to do so in various ways. MPn(Møller-Plesset perturbation), CI (Configuration Interaction), and CC (Coupled Cluster). Among these methods, the CC method can calculate electronic states with extremely high accuracy and is called the gold standard in current first-principles calculations, but it is also very expensive (requires long calculation time).
On the other hand, the DFT method directly considers electron correlations and, although not as accurate as the CC method, it is less expensive and provides more accurate results than the HF method.
Let's take a closer look at the DFT method.
Basics of DFT
The DFT method is now commonly used, called the Kohn-Sham DFT, proposed by Kohn and Sham. In Kohn-Sham DFT, the energy functional is expressed by the following equation.
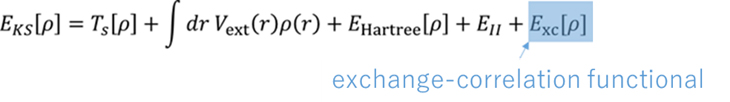
A function takes a value as input, whereas a functional is like a function that takes a function as input and returns a value. For example, the operation of integration can be considered a functional. Integrating a function yields a numerical value called the integral value.
The energy functional can be thought of as such. In the above equation, the density ρ is a function whose value varies with the spatial coordinate r, and inputting it yields the energy value.
The last term Exc in the energy functional is called the exchange-correlation functional, in which the electronic correlations mentioned above are also calculated.
There are many different DFT functionals, and researchers have developed these functionals in an effort to obtain accurate energies for a variety of phenomena and materials. To obtain an energy value, the electron density is required. To do so, we solve the following Kohn-Sham equation.
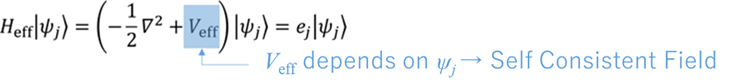
The Kohn-Sham equation is similar in form to the Schrödinger equation, but for one electron, whereas the Schrödinger equation is for many electrons. The above equation is in the form of an eigen-equation, but it is solved using a special technique because the Veff depends on the electron density. This means that the process is repeated until the electron density of the input and the electron density of the output are the same. This procedure is called the Self Consistent Field (SCF) method.
Exchange-correlation functional
In the DFT method, the above-mentioned exchange-correlation functional is the most important. The results will differ depending on what kind of functional is selected. The proposed types of exchange-correlation functional is LDA, GGA, hybrid, and van der Waals (VDW) types.
In LDA, the energy functional is determined by the electron density and is applicable to simple metals, while in GGA, the electron density and its gradient are used to describe the functional, which is the current standard. The PBE functional often used in DFT calculation belong to the GGA.
Hybrid type functional is LDA or GGA type functional plus the exchange energy of the HF method. This is commonly used in quantum chemical calculations, of which the B3LYP functional is a typical example.
The VDW functional is a functional that accounts for intermolecular forces and incorporates interactions between electrons at different positions. A similar approach is the DFT-D functional, which represents intermolecular forces in an empirical function.
Thus, there are many different types of first-principles calculations, and it is necessary to select the appropriate functional for the material or phenomenon under consideration when actually using it.
Table 1. Types of exchange-correlation functional
| Types of functional | Functional | Target and features |
|---|---|---|
| LDA Local Density Approx. |
\(E[\rho]\) | Applicable to alkali metals, etc. |
| GGA Generalized Gradient Approx. |
\(E[\rho,\nabla\rho]\) | Current standard, PBE functional is well-known. |
| Hybrid | \(E[\rho,\nabla\rho]+HFX\) | Such as B3LYP, which is often used in quantum chemical calculations. |
| VDW/DFT-D | \(E[\rho,\nabla\rho,\rho',\nabla\rho' ]\) | Considering intermolecular forces. |
SIESTA
SIESTA is software for DFT calculations. Its name is an acronym for the Spanish Initiative for Electronic Simulations with Thousands of Atoms. As the name SIESTA suggests, it was developed in Spain. It is used all over the world, and a representative paper on SIESTA has been cited more than 10,000 times. SIESTA was originally free for academic use, but since 2016 it is now GPL and free software for commercial use as well.
SIESTA is a registered trade-mark of SIMUNE.
SIMUNE Website >>
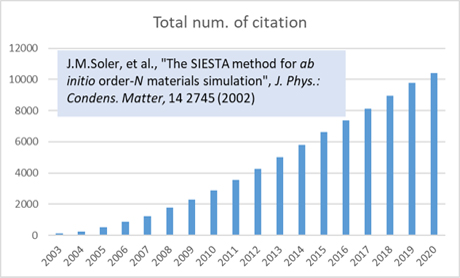Fig.3. Number of citations of representative papers in SIESTA
DFT Software Classification
There are many different types of DFT software. For example, there are two perspectives on the type of software: all-electron calculations or pseudopotentials, and localized basis or plane-wave basis.
First, let's talk about pseudopotentials. A closer look at the structure of an atom shows that it is composed of a nucleus and electrons. Among the electrons, those close to the nucleus are called core electrons and those far from it are called valence electrons. In calculations using pseudopotentials, the nucleus and core electrons together are treated as the pseudopotential, rather than the entire structure being revealed. Therefore, only the valence electrons need to be taken into account in the calculation, which has the advantage of making the calculation more efficient.
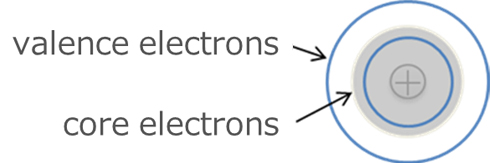Fig.4. Core electrons and valence electrons
As for the difference between atomic(local)-orbital and plane-wave basis, as shown in the figure below, atomic(local)-orbital basis considers electrons only around the atom, while a plane-wave considers many waves spread over the entire cell.
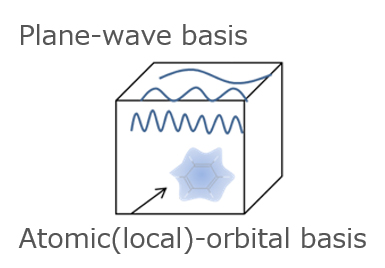Fig.5. Atomic(local)-orbital and plane-wave basis
SIESTA and other software
SIESTA is a software that uses atomic(local)-orbital basis and pseudopotentials.
Gaussian is also based on atomic(local)-orbital basis, but its main use is for all-electron calculations on isolated molecules.
VASP and QUANTUM ESPRESSO are software that use a plane-wave basis and mainly calculate using pseudopotentials. WIEN2k is another known software that uses a plane-wave basis for all-electronic calculations. All-electron calculations are very expensive, but they are the most accurate, so they are used to compare the accuracy of DFT.
Describing the electronic state of matter by plane-waves is very concise as a theory and has been very successful in solid (crystalline) systems. On the other hand, SIESTA uses atomic(local)-orbital basis and considers the distribution of electrons only around atoms. This makes it particularly efficient for calculations involving vacuum regions, such as interfacial systems. SIESTA also implements several VDW functionals, which are advantageous in the calculation of intermolecular interactions.
In addition, the low memory consumption makes calculations involving 100 to 1000 atoms relatively easy to perform. This will be an advantage for large-scale calculations (e.g., molecular adsorption on solids and nanocomposites), which will become increasingly necessary.
This is an overview of first-principles calculations and the position of SIESTA. If you have any questions, please feel free to ask.
