- Full Atomistic MD
- Optical / Electrical / Magnetic
- Materials Science
Dielectric dispersion of water in the GHz frequency range (2)
Purpose and method
The complex permittivity of water has been evaluated by applying an external electric field with full-atomistic molecular dynamics method. By applying a periodically oscillating electric field \( E(t) = E_0\cos (\omega t) \) to a dielectric material, polarization (Eq. (1)) is induced in the dielectric with the phase delay \( \varphi\).
\[ P(t) = P_0\cos (\omega t + \varphi) \]
…（1）
From the relationship between the electric field and polarization in this case, the complex permittivity (real part: ε’, imaginary part: ε”) is expressed in Equation (2).
\[ ε{\small'}(\omega) = 1 + \frac{4\pi P_0\cos\varphi(\omega)}{E_0} \]
\[ ε{\small''}(\omega) = \frac{4\pi P_0\sin\varphi(\omega)}{E_0} \]
…（2）
VSOP was conducted to obtain the response of the polarization at each time by applying the oscillating electric field to the water model. The model shown in Figure 1 was used to apply the electric field to the Z-axis (longitudinal direction). Because the dielectric constant depends on the frequency 𝜔 of the electric field, the complex permittivity was obtained for each frequency by specifying several frequencies. The SPC/Fw was assigned for the force field of water and the NVT ensemble was used at 300 [K] temperature.
Figure 1. The model of water
Simulation result
The response of the polarization (P calc) to the input (E) of an electric field of frequency 6.5 [GHz] is shown in Figure 2. The calculated polarization response was fitted by equation (1) and the phase delay was evaluated. The delay of polarization response is confirmed.
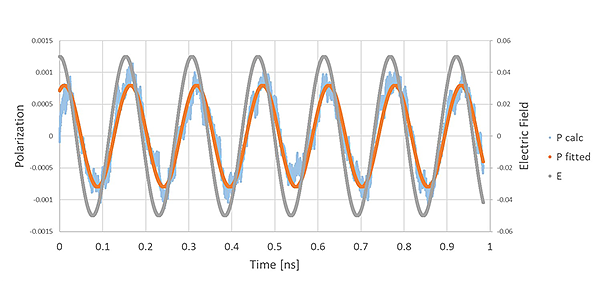Figure 2. The polarization response to the oscillating electric field
By evaluating the phase delay at other frequencies as well, we were able to evaluate the complex permittivity of water at each frequency, as shown in Figure 3. The results are in good agreement with those of the dielectric dispersion evaluated from the dielectric relaxation function. By using an external electric field, it is possible to directly evaluate the dielectric permittivity at arbitrary frequencies.
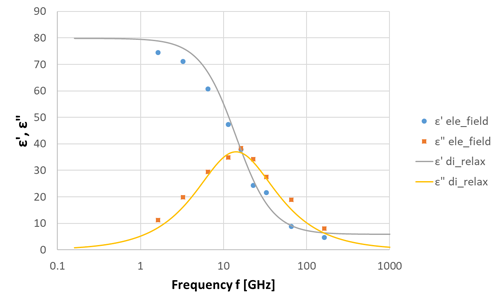Figure 3. Dielectric dispersion of water
